1. SQL Recipes
2. Smoothing Data
3. Calculating Exponential Moving Average with Recursive CTEs

Calculating Exponential Moving Average in SQL with Recursive CTEs

Similar to simple/weighted moving averages, exponential moving averages (EMA) smooth out the observed data values. The difference is that these methods use the previously calculated EMA value as a basis rather than the original (non-smooth) data value. Since EMA builds upon itself, all previous data values have some effect on the new EMA, though the effect diminishes quickly with time.

1. The math

The equation for EMA is recursive, i.e., new values use the previously calculated EMA values:

where,

Variable	Explanation
	Current observation at .
	Current EMA at , i.e., EMA to be calculated.
	Smoothing factor that determines how much weight we give to the most recent observed value versus the last calculated EMA. is between 1 and 0. A value of 0.5 weighs both sides equally.
	Last calculated EMA, with a special value of to be equal to the first data point.

2. The SQL with PostgreSQL recursive query

To implement this in SQL, let's take an illustrative example: our data is sales data that shows a strong seasonal component. Moreover, it's trending higher period-over-period.

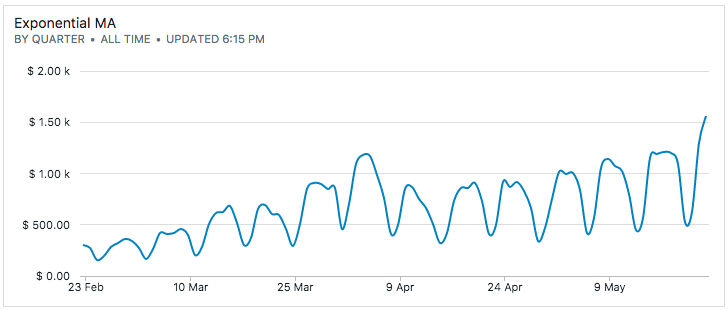
The table has two columns: dt a timestamp and sales as a number.

To solve the recursive equation, we'll use PostgreSQL's recursive queries. PostgreSQL queries can have a WITH clause, that allows you use statements – know as common table expressions (CTE) – that behave like temporary tables that only exist during the execution of the query.

If the CTE contains a recursive component, that's a recursive query. Recursive queries are useful to query data that demonstrate a hierarchical nature.

To define a recursive query, we need two parts – an initial query that is non-recursive and the recursive part. The general form of a recursive query is as follows:

with cte_name (
    cte_query_definition -- non-recursive portion
    union [all]
    cte_query_definion  -- recursive portion        
) 
select * from cte_name;

For the non-recursive portion, we will pick out the first row of the sales data. We can get the first row by numbering the results with the row_number window function and adding a WHERE clause:

select * from (
    select dt, 
        sales, 
        row_number() over ()
    from sales_data) w
where row_number = 1;

For the non-recursive portion, we use a self-join with the rows offset by 1 to get the previous row (we additionally re-factor getting the columns from the table as t)

with t as (
    select dt, 
        sales, 
        row_number() over ()
)
select * from t 
join t t2 on t2.row_number = t.row_number - 1;

Now, it's a matter of filling in the equation to calculate EMA, a UNION with the non-recursive part and making sure both portions have the same number of columns.

with recursive t as (
    select dt, 
           0.5 as alpha,
           row_number() over (),
           sales
    from sales_data        
),

ema as (
    select *, sales as sales_ema from t 
    where row_number = 1

    union all

    select t2.dt, 
           t2.alpha, 
           t2.row_number, 
           t2.sales, 
           t2.alpha * t2.sales + (1.0 - t2.alpha) * ema.sales as sales_ema
    from ema
    join t t2 on ema.row_number = t2.row_number - 1
)

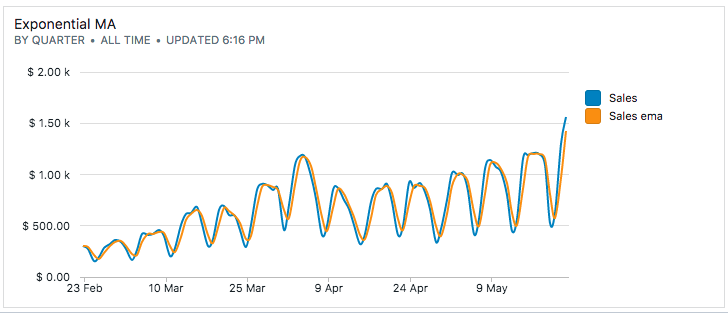
select dt, sales, sales_ema
from ema;