Percentiles are often used to find outliers and explore the distribution of data. For instance, you want to make sure 95% (and a stricter 99%) of your website visitors meet a certain response time. Let’s look at some of the challenges of computing percentiles on big data…

The need for percentiles

Why do even need percentiles? Why not simply use averages, which are simpler to compute and reason about. Averages are inadequate and often misleading because they are drastically skewed by outliers.

If you care about using data to guide pricing tiers, knowing the distribution of data is critical. Averages are not very useful in this scenario.

The Classic Algorithm

def median(data):
    sorted_data = sorted(data)
    data_len = len(sorted_data)
    return 0.5*( sorted_data[(data_len-1)//2] + sorted_data[data_len//2])

The classic algorithm is usually given to beginner programmers as a homework assignment. The above snippet computes the 50th percentile (median) of the input data. It does this by sorting the data, calculating the length and returning the middle element (and accounting for even array lengths.)

The killer is the sort step.

Challenges

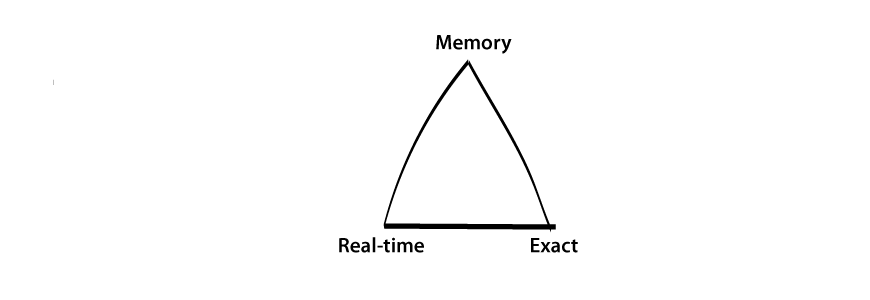
When trying to scale a percentile computation, you have three algorithm design choices. The top-level decision is whether your data fits on one machine or not.

• Small data, fits on one machine, can compute exact percentiles
• Big data, does not fit on one machine, batch computation for exact percentiles
• Big data, does not fit on one machine, real-time computation for approximate percentiles

The T-Digest algorithm

The t-digest algorithm is an innovative algorithm implemented in many popular machine learning and data mining libraries. The algorithm comes with interesting properties for computing percentiles:

• for small data, the percentiles can be highly accurate
• extreme percentiles like 99th are more accurate than percentiles like median (50th percentile)
• for big data, the algorithm trades memory for accuracy

Implications of approximation

How far can you go with approximate calculations? For practical calculations like burstable billing, or honoring service level agreements, real-time calculations are far more important than 100% exact calculations. Consider a 0.1% error in approximating 95th percentile bandwith usage for the month:

• an exact value of 200.1 megabits per second, which could take hours to compute
• an approximate value of 200.1±0.2 megabits per second, which takes milliseconds to compute

As you can see, an approximate calculation does the job and is readily useful.

Photo Credit: generated.